第61回　最適生産

　生産関数にもいろいろな型があることを前回みました。

　今回は、生産者論の最後なので、前回出てきた「コブ＝ダグラス型生産関数」を使って、費用制約の下での最適な生産要素の配分と生産量を考えます。

　生産関数は前回みたので、ここでは、費用関数を定式化してみます。

TC　＝　ｒK　＋　ｗL　　・・・・・・・・①

　TCは、等費用（総費用）曲線を示しており、ｒは、資本のレンタル料、Kは、資本量、wは、賃金率、最後のLは、労働量です。ここでは、総費用を、資本にかかった費用（利子なども含めている）と労働費用の総合計と考えています。ここで①式を、②式のように、変形します。

　K　＝　－(w / r) L ＋　TC / ｒ　　・・・・・・・②

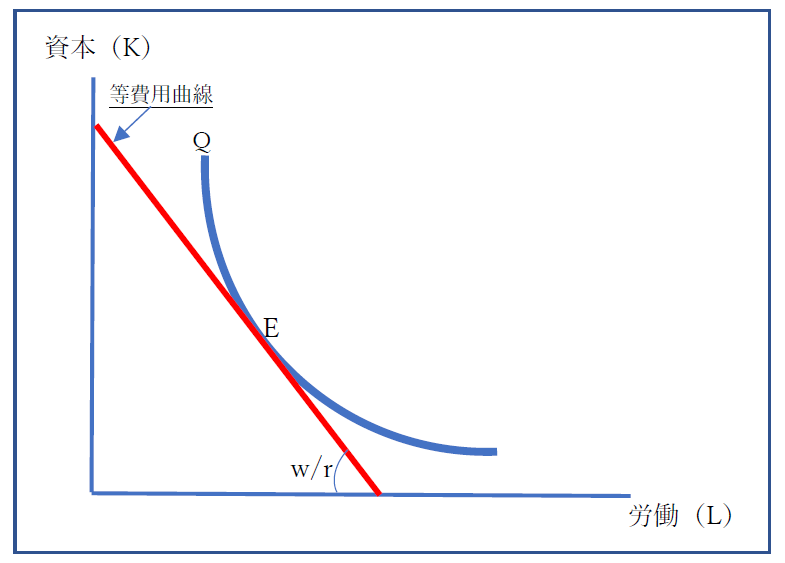
　この②式は、図表でいえば、赤い直線の「等費用曲線（iso-cost curve）」です。切片が、（TC/r）で、傾きが（ｗ/r）です。

　ここで、等生産曲線(Q)と等費用曲線が接している点が、E点です。等費用曲線は、最大の費用を示しており、それより下は、費用が余っている状態であり、それより上は、費用が足りない状態です。その費用の制約下、最大の生産量が、E点です。

　そして、E点における技術的限界代替率（MRTS）と、等費用曲線の傾きが等しくなっています。

　よって、最適な生産点の条件は、

　MRTS　＝　ｗ/r 　・・・・・・・・③

　となります。