マクロ経済学第83回　ソロー・スワンモデル

　今回は、新古典派の成長経済理論である「ソロー＝スワンモデル(Solow=Swan model)」を考えます。

　前回のハロッド＝ドーマモデルと異なり、資本と労働との間に代替関係があり、資本レンタル料（利子率）が高いときには、相対的に安い労働力を利用し、賃金率（時給）が高いときは資本を多く利用するということです。

　まずは、定式化を試みます。

　第一式は、マクロ的生産関数を表していますが、成長会計でもみたように、コッブ＝ダグラス型生産関数を用いています。第二式は、第一式の両辺をLで除したものです。すると、一人当たりの所得（y）となります。第三式は、一人当たりの資本装備率（資本労働比率）を示しています。第四式を、一人当たりの所得と一人当たりの資本装備率に置き換えたのが第五式です。第六式は、労働力の増加は、「労働増加率×労働力（量）」で、第七式は、資本の増加が、「貯蓄率×GDP」で計算されています。これらより、第八式が、ソローの方程式となります。左辺の一人当たりの資本装備の増加分は、「貯蓄率×一人当たりの所得」から、「労働増加率×一人当たりの資本装備率」を引いたもので表されます。

　これらを、図化したものが、下図表です。

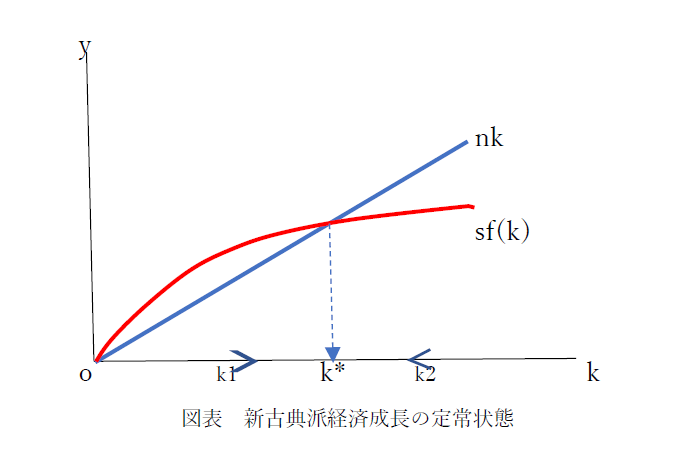
　図表１の横軸は、一人当たりの資本装備率（資本労働比率）で、縦軸は、一人当たりの所得（生産）です。

　ここで、長期均衡は、ｋ^＊の位置で、定常化します。

　その理由を書きます。

　まず、一人当たりの資本装備率が、k = k1であった場合は、sf(k) > nk 、なので、 △kは、プラスとなり、一人当たりの資本装備は、一層増加します。逆に、k= k2 の状態であれば、△kは、マイナスとなるので、一人当たりの資本装備は、減少します。結果、k*のところで、長期的に均衡すると考えるのです。

　この場合、一人当たりの貯蓄率（s）が高まると、より一層の資本装備率が高まり、一人当たりの国民所得は上昇します。

　また、労働成長率（n）が高まると、資本装備率が低下し、国民所得も減少することになります。