AI経済学　第13回　ＡI的費用関数のモデル

　企業活動において、費用問題はもっとも重要な問題のひとつです。

　ところが、ミクロ経済学では、費用関数は、きわめて簡素に想定され、定義されています。

　標準的なテキストでは、総費用は、固定費用と可変費用（変動費用）の和とします（当コラムミクロ経済学第37回参照）。

　また、短期費用概念と長期費用概念に分け、前者は、固定費が変わらない状況をいい、後者は、固定費用も変化し、変動費化した場合を考えます。

　ここでも、必ずしもミクロ経済学のロジックを取らず、いわば、ＡＩ的な費用関数を考えてみたいと思います。

　ただし、ミクロ経済学における費用関数の形状は、逆Ｓ字を取ると想定することが大半です。これは、生産の初期段階では、費用はむしろ効率的となり（限界費用が逓減する）、その後、費用は非効率的になるとみるからです（限界費用が逓増するとみます）。かならず、そうなるかどうかは、企業が属している産業や業態、および個別企業の都合でいろいろなことが考えられますが、一般的には、逆Ｓ字型の曲線とみることはもっともらしいといえます。

　この逆Ｓ字型に近似している関数は、ロジット関数とみることができます。

　この関数を簡略に説明すると、確率Ｐで生起する現象Ａにたいして、Ａが生起する確率と生起しない確率の比（オッズとよぶ）を、対数にとったものです。

　数式で表すと、

　f(p) = log (p / (1 – p))

 となります。

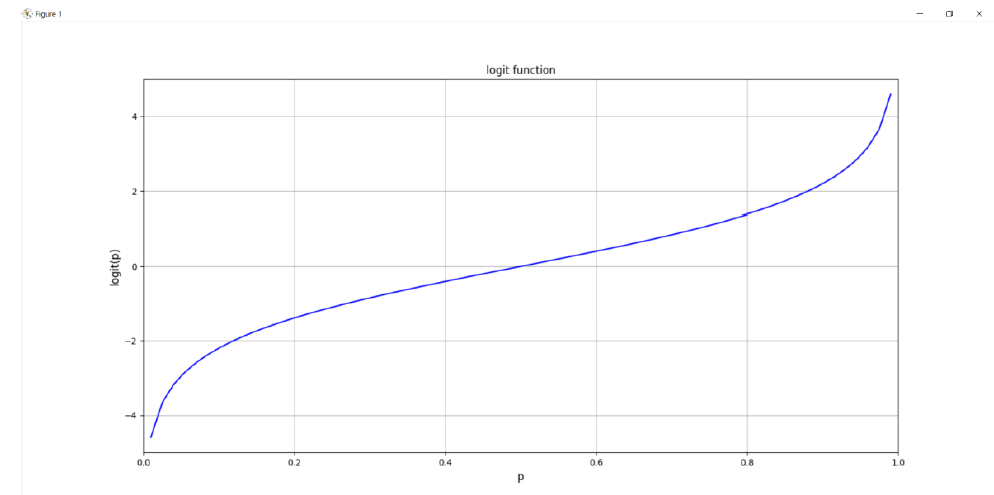
　この関数をPython言語で描画すると、図表１のようになります。

　この場合、Pが0に漸近すると、－∞となり、Pが1に漸近すると、+∞となることを意味しています。Pが0.5のときには、ロジット値は、0となります。

　これはあくまでも理念モデルですが、逆S字型関数の本質は表れています。