第11回　需要関数の導出

　今回は、需要関数を導出してみます。

　個人の需要関数は、ある財に対して、価格が高いときには少ない需要で、価格が低くなるとたくさん買いたくなります。よって、個人の需要関数も図表のように、右下がりの曲線となります。

　市場は、無数の需要者の参加でできあがっていますので、個人の需要をすべて横に足し合わせたものとなります。これは無数の人の全体需要ですから、ずいぶんと大きなものになり、右上に位置することになります。

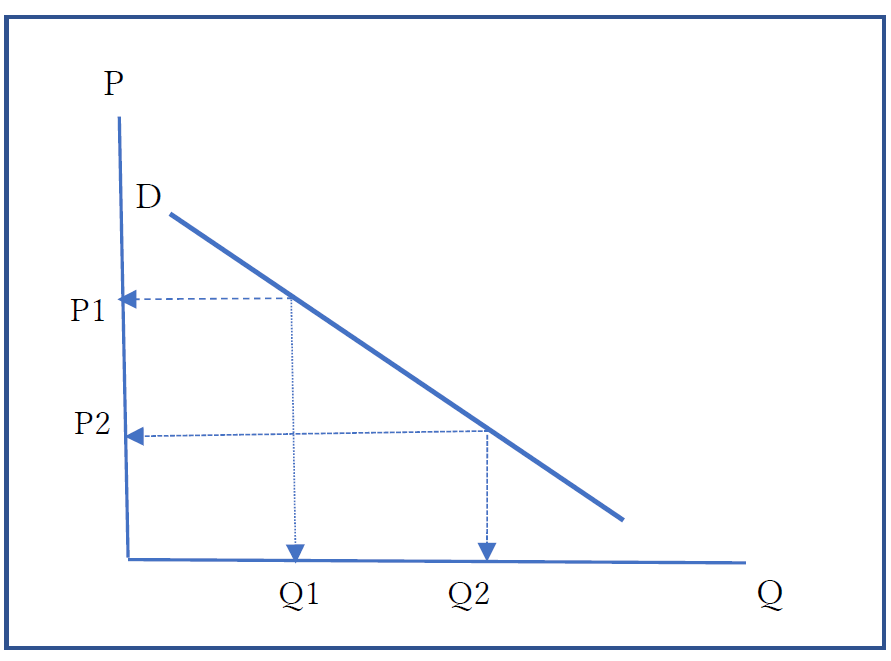
　図表は、全体需要（市場におけるすべて需要）を示しています。

　数式としては、

　Ｄ　＝　ｆ（　Ｐ　）

　または、

　Ｄ　＝　－　a・Ｐ　＋　ｂ

　と表します。　Ｄは、需要量で、ｆは関数、Ｐは価格を意味しており、a、bは、常数です。

　ここで、Ｐ１は、ずいぶんと高い価格のときですが、このときは、需要量はＱ１しかありません。これに対して、Ｐ２のような安い価格では、需要量はＱ２のように大きくなります。直線は、2点が決まれば描けるので、ここでも２点で説明しました。

　ここで、需要曲線の傾きが緩やかな場合（水平に近いとき）は、需要の価格弾力性が大きく、傾きが急なとき（垂直に近いとき）は、需要の価格弾力性が小さいといいます。これに関しては、消費（者）の理論のときに詳しく述べます。