第63回　効用の1財モデル

　ミクロ経済学は、消費者と生産者という２つの経済主体の行動およびその取引を記述する社会科学の一領域です。

　すでに、市場論や生産者の理論は議論しましたので、前回に引き続き、消費者の理論を何かに分けてお話しします。

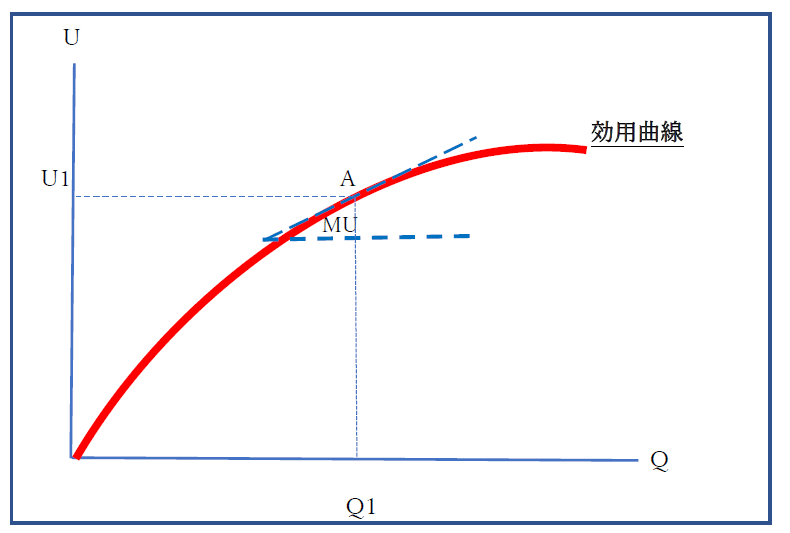
　ここでは、ある財（1財）における、消費量（Q）とその効用の大きさの関係を考えます。横軸に、消費量をとり、縦軸に、効用をとっています。

　すると、原則的に、上に凸の曲線として「効用曲線（utility curve）」を描きます。

　定式化すると、

　U　＝　U（Q）　・・・・・・・・①

　となります。

　これは消費量（Q）に応じて効用（U）が決まるということを示しています。

この効用関数には、２つの意味が含まれています。

　その第一は、消費量が増加すると、効用も増加するということです。しかも、消費量がいくら増えても、効用には限界がないとみます。これを「非飽和の仮定（assumption of desaturation）」といいます。現実的には、個々人の満足にも限りがあるでしょうが、理論モデルとしては、そう仮定します。

　第二は、消費量が一単位増加するごとの効用の増分のことを、「限界効用（marginal utility）」といいますが、それが次第に逓減することを、「限界効用逓減の法則（law of diminishing marginal utility）」といいます。これは現実的な生理現象に馴染みます。たとえば、喉が渇いたときに、最初の1杯目の水は大変においしく感じますが、2杯目、3杯目となると、徐々に効用（満足感）は小さくなるのが普通なので、常識にかなっています。

　この限界効用(MU)を定式化すると、

　MU　＝　ΔU / ΔQ　　・・・・・・・②

　となります。

　なお、この限界効用は、図表でいえば、青い破線の角度で表されます。または、A点での接線の傾きと同じことを意味しています。

　効用曲線上を右にいけばいくほど、その点での接線の傾きは小さくなります。