第69回　ナッシュ均衡と囚人のジレンマ

　今回から、何回かにわたって、ゲーム理論の主なゲームをみていきます。

　その第一回目は、「囚人のジレンマ(Prisoner’s dilemma)」と呼ばれているゲームです。ほぼすべての教科書に出ているケースです。

　ここでは利得表を使って、解法手順を示していきます。次回以降は、自身で同様な手順で解法してください。　

　ここで、囚人のジレンマのゲームの前提としての構成要素をみてみましょう。

　プレイヤーは、容疑者2名とします。どんな事件でもいいのですが、ここでは、懲役刑が課せられるぐらいの重大な事件を起こした容疑者とします。この2名は、別々の取り調べを受けており、両者は、隔離されているとします。これは両者の間に連絡が取れない状況であることを意味します。

　つぎに、容疑者がとりうる行動は、自白か黙秘かのどちらかとします。これはゲーム理論における行動選択のオプションに相当します。

　最後に、図表１のような利得表があるとします。この見方は、（Xの利得、Yの利得）となっています。なかの数字は、原則として意味をもちません。たとえば、晴れの日は、「１」で、雨の日は、「－１」で、曇りの日は、「０」という数字が与えられているときには、この数字は、現象を示している記号にすぎないのです。ただし、ここの場合は、数字に意味を持たせています。１０は、１０年の懲役刑であり、５は、5年の懲役刑であり、０は、無罪を示しています。

　ここで、ナッシュ均衡であるかどうかを判断します。

ナッシュ均衡とは、「他のプレイヤーの戦略下ですべてのプレイヤーが最適な戦略をとりあっている状態」のことをいいます。

　ここでは、X容疑者も、Y容疑者も、相手の戦略に対して、もっともよい戦略をとりあっていることです。

　では、解説していきます。

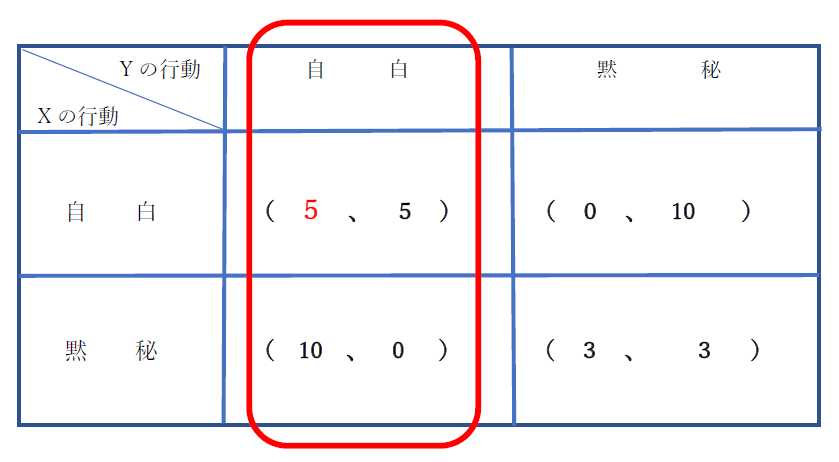
　まず、Y容疑者が、自白という行動を選択すると考えます。これを前提とすれば、X容疑者は、自白をとれば、5年の懲役、黙秘をとれば、10年の懲役となるので、自白の方をとります。ここでは、採用するほうを、赤い数字として表示しています。

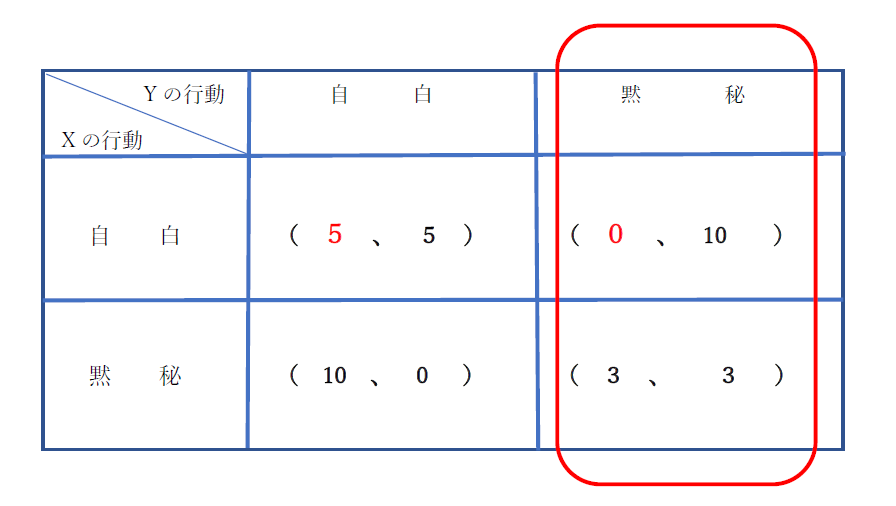
　つぎに、Y容疑者が、黙秘をとると考えます。すると、先と同様に、Xにとってよい行動は、自白です。

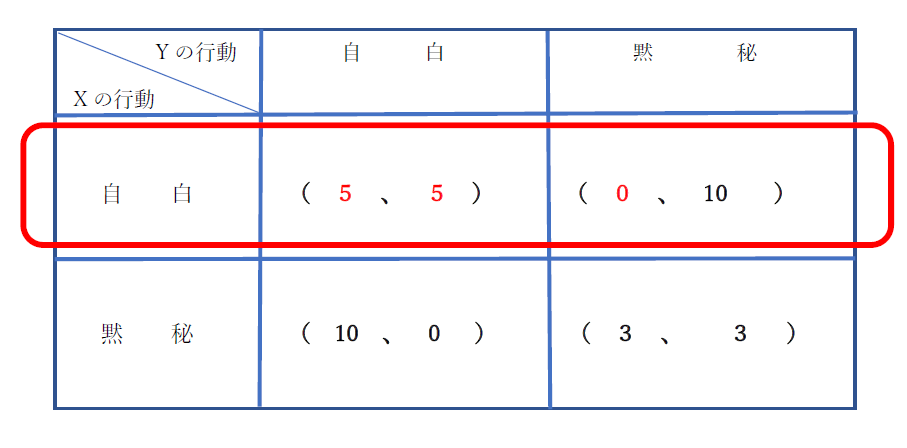
　 今度は、X容疑者の行動を前提に、Yがとりうる行動をみます。Xが自白をする場合は、Yも自白を選んだ方がとくです。

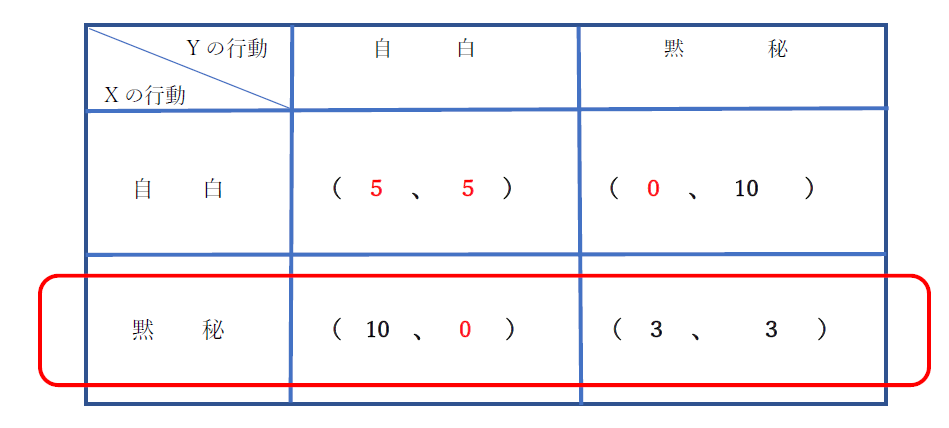
　同じように、Xが黙秘を選ぶと考えた場合、Yは、自白を選ぶと考えます。

　ここで、先のナッシュ均衡の定義に戻ると、すべてのプレイヤーが相手の行動を前提として、自身のもっとも有利な選択をして、最適な戦略をとりあっているのは、（自白、自白）という行動の組み合わせです。図表では、両者ともが赤い数字となっている組です。他の組は、一方がとりえても、片方がとりえない組、または、両方ともとっていない組となっています。

　しかし、このケースでは、X容疑者もY容疑者も、（黙秘、黙秘）をすれば、両者とも3年の懲役で刑期が短かったのです。すなわち、囚人のジレンマは、ナッシュ均衡ではあるが、パレート効率的ではないことが分かります。

　なぜこのような事態となったのでしょうか。

　それは、今回は、容疑者が別々に取り調べを受けていて、連絡がとれなかったからです。もっというと、相手が自白すると、自身は重い刑が科せられるので、自白しないという情報を得られないがために、両方が自白することを選んだのです。

　逆にいえば、互いが話し合え、協調（同調）することができれば、もっと都合のいい結果を得られることを示しています。

　この「囚人のジレンマ」というゲームは、個人や企業が、競争することなく、協調することによって、もっとよい結果を得られる可能性を示唆しているのです。