
マクロ経済学第86回 AKモデル
今回から、経済成長モデルのなかで、新古典派経済成長モデルの発展形ともいえる「内生的経済成長モデル」を考えます。
その出発となる「AKモデル」をここでは考えます。
前回のコラムのなかで、技術進歩や人口成長率が外生的であること、および、資本投資のみではいずれは経済成長が止まることを述べました。AK理論は、それをどのように理論的に克服すべきかを考えたものです。
今後の記述は、C.I. ジョーンズ(Charles I. Jones)の著書『経済成長理論入門』(香西泰監訳、日本経済新聞社、2000)を使って考察していきます。なお、原著名は、”Introduction to economic growth”です。
ここで、コッブ=ダグラス型生産関数をおさらいしてみましょう。
Y = F(K, L) ・・・・・・・・・・・①
この式を書き換えると、
Y = AKαL(1-α) ・・・・・・・②
でした(ただし、Aをどこに配置させるかでいろいろなタイプに分けることができます)。
ここで、α=1であるとすると、第二式は、
Y = AK ・・・・・・・・・・・・・③
となります。
AK理論は、この表現形から名前がきています。早い時期にこの理論を展開したのは、「レベロ(S. Rebelo)」(1990),”Long Run Policy Analysis and Long Run Growth”といわれています。
なお、αが1ということは、労働力に対する労働配分率がゼロということであり、GDPの成長は、資本(K)およびA(技術進歩)が担うということを意味します。
ここで、資本蓄積方程式を定式化すると第四式となります。

左辺の資本形成量は、右辺第一項の資本量から、第二項の「減耗率×資本量」を引けばでます。減耗量とは、資本の減少量のことです。簡単にいえば、生産設備などが老朽化または劣化することを言います。
この第四式の両辺をKで除すると、

となり、これに第三式を代入すると、
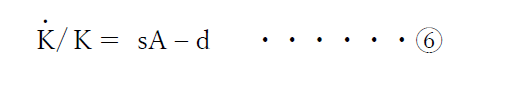
となります。
さらに、第六式を対数にとり微分すると、
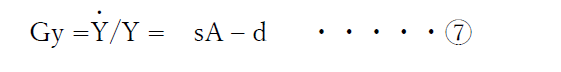
となります。
ここで解説を加えると、左辺は、GDPの成長率です。それが、右辺の二つの項の関係で決まります。sAは、「貯蓄率×技術進歩」で、Aが定数としても、sが増加することによって、結果、技術進歩は増大します。さらに、ここでの技術進歩は、様々な要因を含みます。人的資本、金融資本、研究開発資本、インフラ資本などから生み出される知識・技術の総計、主に「インタンジブルズ(Intangibles Assets)」です。そこから、減耗率を引いたものがGDPの成長率となります。s(貯蓄率、それがすべて投資に回るとすると投資率)が増加すれば、または、d(資本減耗率)が減少すれば、経済成長率は高まることになります。
まとめますと、このAKモデルでは、第二式から、広義の資本が増加する限り、経済成長は止まらないということを意味しています。
第七式でいえば、貯蓄が投資に回り、それとAと乗した値が、資本減耗率よりも大きければ、経済は成長し続けることを意味しています。


