AI経済学　第9回　需要関数の移行のソフト化

　本コラムのミクロ経済学の第12回で、需要関数（曲線）の移行に関して述べています。

　これをAI用言語という場合もあるPython言語を使って、シミュレーションしてみたい（厳密にはＡIアルゴリズムも扱えるプログラム言語）。

　経済学は、多くの学習者から、どうもなじみがなく、分かりにくいという批判がある。たしかに、理論の前提が非現実的で、かつその条件が厳しいので、現実の経済現象や行動とはかなりかけ離れていることも確かです。

　とはいえ、理想解を見つけ出すためには、いたしかたないので、とくにミクロ経済学は、そのような手法（表現方法）を採用しているのです。

　このとっつきにくいミクロ経済学における理論を、シミュレーションソフトを作って、シミュレートする意味は何でしょうか。

　まずは、直感的に視覚化されるので、変数や方程式の意味が理解しやすいことが考えられます。つぎに、初期値やパラメータを変化させることによって、解がどのように変化するのかもわかります。そもそも変数はそれで十分なのか、または過剰ではないかなどの理解も進みます。

　また、シミュレーションは、将来予測をするために重要です。

　その予測に基づいて、なにをどのように改善・工夫をすべきかもわかります。

　シミュレーションの意義や課題は、今後詳細に議論するとして、ここでは、完全競争市場における需要関数の移行を考えました。

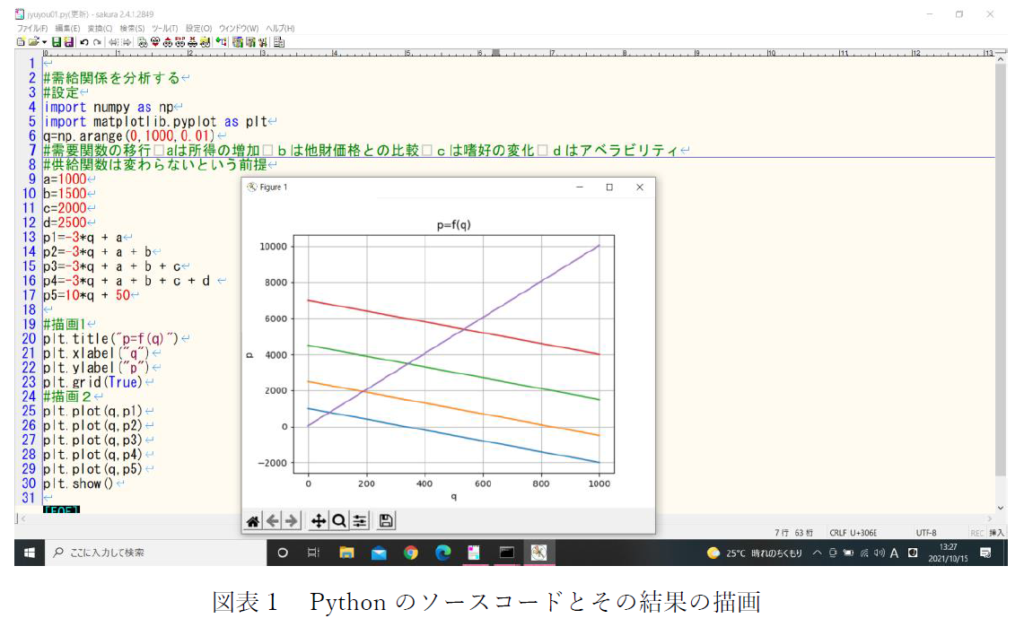
　ここでのPythonのソースコードをみると、需要関数の以降の変数として、４つ挙げています。

aは、所得の増大で、ｂは、他財（補完財や代替財など）との価格をとり、ｃは、嗜好の変化、ｄには、アベイラビリティ（資金の入手の容易さなど）を設定しています。ほかにも様々な要因が考えられます。たとえば、天候の影響や経済動向などです。入れようと思えばいくらでもいれられるということもシミュレーションのいい面です。ただし、それぞれの変数の初期値はここではまったくの任意（ダミー）です。これらは、現実の経済の観察から値が決定されることが望ましいでしょう。

　また、経済学は、静学と動学とがあり、ここでは、基本的に採用されている静学的表現でソースが書かれています。動学的に表現する場合は、時間発展方程式をつかった表現の方が望ましいと思います。これは今後書いていきます（ソースはすでに作成されていますので）。

　図表１の右下がりの線が、需要曲線で、下位から順番に要因を付け加えたものです。供給関数は、右上がりの線です（ここでは前提としました）。

　やはり、様々な要因が付け加わると、交点（均衡点）が、上方に移行していることが分かります。それに従って、均衡量と均衡価格も上昇していくことを示しています。