ＡI経済学　第14回　AIによる故障診断費用

　企業活動において、費用問題はもっとも重要な問題のひとつであると、前回のコラムでは書きました。

　この費用には、土地や建物などの固定資本や、原材料や光熱費や労賃などすべてが含まれます。これを定式化することは、簡単ではありませんが、企業はそれぞれの費用をどうにかして管理していることも事実です。

　ここでは、AIによる故障診断プログラムの費用を考えてみたいと思います。

　このシステムを開発するときに、まずもって重要なことは、故障が時間の推移によってどのように変化するのかを見極めることです。言い換えると、どのような近似関数として、故障率を考えるかということです。

　なぜなら、貴重な生産資源である工具や生産機械が故障すると、その生産性は落ち、修理または取り換えとして多額の費用がかかるからです。

　そこで、いろいろな関連論文を読んでみると、故障推移（ここでは、故障を摩耗、変形、損傷などすべてを含む概念としています）は、多くのパターンがあることが分かりました。

　たとえば、工具の場合の摩耗は、だいたい指数関数的に増加します。ただし、素材や活用状態や環境状況によって、その変化や曲線の位置は大きく変わります。

　それに対して、複合的な製品の故障率は、バスタブのような形状として一般的に想定されています。

　さらには、今度、お話しするロジスティック曲線のような摩耗劣化のパターンもあります。

　そのなかで、もっとも多くのパターンは、前回お話しした、ロジット曲線のような形状です。まさに、逆S字型曲線です。

　ただし、その故障個所が複数存在する場合、その故障原因は複合的であり複雑系であるといえます。

まさに、AIによる故障診断が奏功する問題であると考えられます。

　ここで、AI診断ソフトウエアを開発して、企業の利潤がどのようになるかに関する方程式を簡潔に書いてみます。

　π= TR – TC ・・・・・・・・・①

　　（π：利潤　　TR : 総収入　　TC : 総費用）

  π= TR – TC(Cg + Ca) ・・・・・②

　　（Cｇ：一般生産費用　　Ｃａ：ＡＩ費用）

　ここで、一般式は①ですが、それに、ＡＩに関する費用を入れたものが、②式です。

　ここで、ＡＩ投資（Ｃａ）によって、その費用増分以上に、Ｃｇ（一般生産費用）が低下すれば、利潤は増大します。ＡＩの投資が利潤拡大に寄与するように、ＡＩ投資は行われるべきことが分かります。

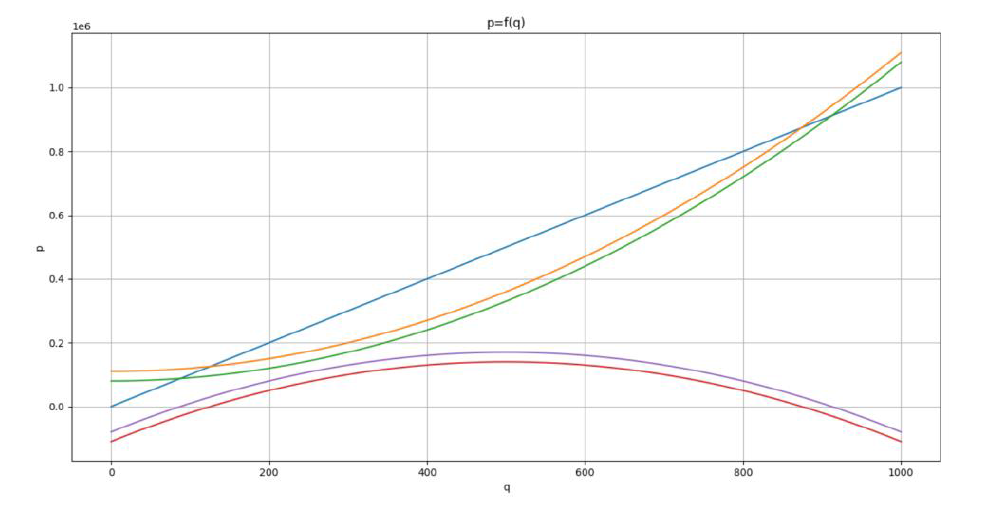
　それらを図示したものが図表１です。

　横軸に、生産量（ｑ）をとり、縦軸に価格（ｐ）をとっています。

　青い直線が、収入線（ＴR線）です（ここでは、完全競争市場における価格が一定という場合を想定しています）。

　それに対して、下に凸のオレンジの線は、ＡＩ投入前の費用関数で、緑の線は、投入後に総費用が低下した場合の曲線です。

　これによって、利潤曲線（上に凸の線）は、赤い線から紫の線に上方移動しています。すなわち、利潤が拡大したことを示しています。

　ここの議論では、故障に対する費用問題を取り上げましたが、ＡＩはあらゆる企業費用の低下に貢献すると考えられます。

　今後は、それぞれの費用の削減のメカニズムをまた書いていきます。