マクロ経済学第4回　ライフサイクル仮説

　これまでにいくつかの消費関数モデルを示してきましたが、今回は、モディリアーニ（Franco Modigliani; 1918-2003）が唱えた「ライフサイクル仮説（Life Cycle Hypothesis）」を考えていきます。

　この仮説では、消費は、その人が生涯で得る収入の大きさによって決まると考えます。ただし、将来の所得は、不確実ですが、予想して生涯収入を計算するとみます。

　本来、経済学におけるモデルは、過去の経験や実証データから得られた知見を総合して、方程式を作り出します。そして、現実のデータと比較をしてモデルを検証したり、モデルを精緻化していきます。これをモデル・ビルディングといいます。

　ここでは、もっとも、簡素なライフサイクル仮説を示します。そのほうが理解が明快となるとともに、その後に、より複雑なモデルを考えればいいからです。

ここで、図表と式を導出しておきます。

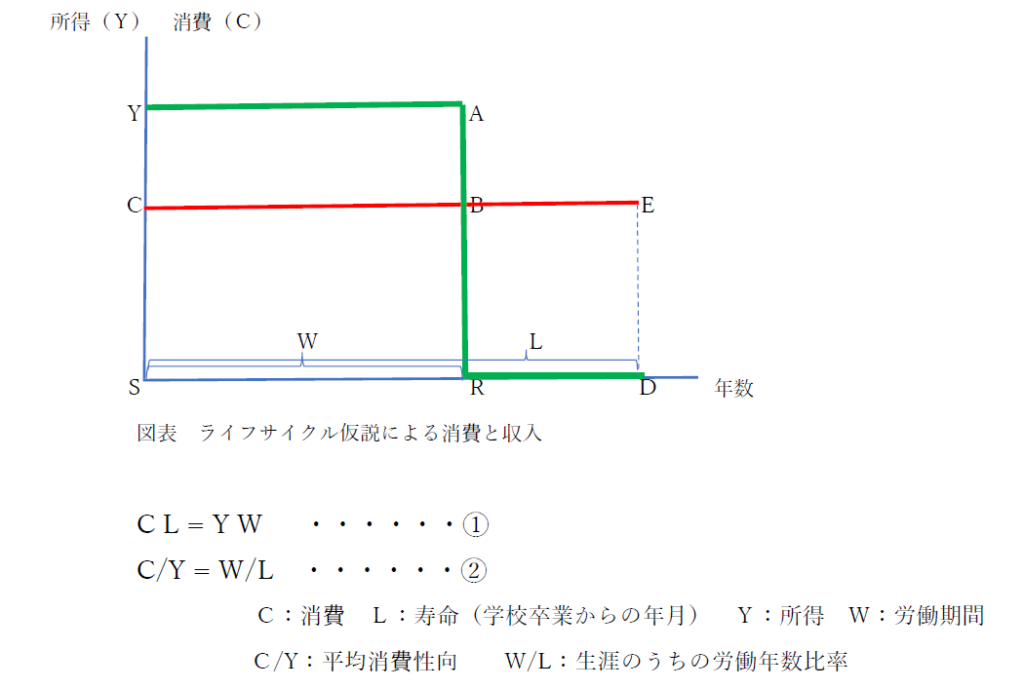
　　図表の説明をすると、Ｓは、学校卒業年です。Ｒは、退職年です。Ｄは、死亡年です。Ｗは、労働期間で、Ｌは、学校卒業から死亡までの期間を表しています。所得曲線は、緑の線です（Ｒ点で屈曲しています）。消費曲線は、赤い線です。

まず、簡素なモデルのために、前提を書いておきます。この場合、利子率はゼロとします。また、譲り受けた資産はないとします。消費も所得も生涯を通じて一定とします。現実では、歳を経るにしたがって、消費も所得も大きくなるのでしょうが、ここでは、変わらないとします。さらに、労働年限が過ぎると、収入はゼロとします。また、生涯収入をすべて使い果たすモデルです。図表の原点は、学校を卒業した時からとっています。

　この場合、ある人の生涯収入は、図表でいえば、四角形ＹＡＲＳです。それに対して、生涯消費は、四角形ＣＥＤＳです。四角形ＹＡＢＣは、働いていたときの貯蓄額を示しています。また、四角形ＢＥＤＲは、収入がゼロの中、貯蓄を切り崩して生活をしていることを表しています。

　ここで、数式の説明します。第一式は、左辺（ＣＬ）が、生涯消費を示し、右辺（ＹＷ）が、生涯収入を示しており、それが一致するとみているのです。第二式は、平均消費性向（C/Y）で、所得に占める消費の割合ですが、それは、生涯でどのくらい働けるかで決まることを示しています。日本では定年が決まっており、日本人の平均寿命もある程度分かっています（ただし、定年の延長や平均寿命も延びていることもここに入れることができます）。

　すると、収入が一定であれば、どの程度の消費がふさわしいかが決まります。または、消費が一定であるとすると、そのためにはどの程度労働を強化しなければならないかが分かります。どちらにしても、平均消費性向は、一定ということになります。