第34回　公共財の供給

　公共財は、財の非競合性という特徴から、私的財とは異なる需給関係を作り出します。

　私的財では、全体需要曲線と供給曲線によって、均衡価格（P*）が形成されますが、個別需要者も同じ価格で取引します。ここで、Aさんの取引価格をPaとし、Bさんの取引価格をPbとします。完全競争市場を想定しているので、無数の需要者が存在しているのですが、ここでは2人のモデルで考えています。

私的財の取引では、

　P* = Pa = Pb

が成り立ちます。すべての個別需要者が同じ価格（均衡価格）で取引するからです。これを別の面で言い換えると、それぞれの個別需要は、水平に足し合わされるといえます。

　これに対して、公共財の場合は、さきにも述べたように非競合性により、同時消費（等量消費）が可能なので、それぞれの需要は、垂直方向に足し合わされるとみます。それを示しているのが、下図表です。これも2人のモデルで考えています。

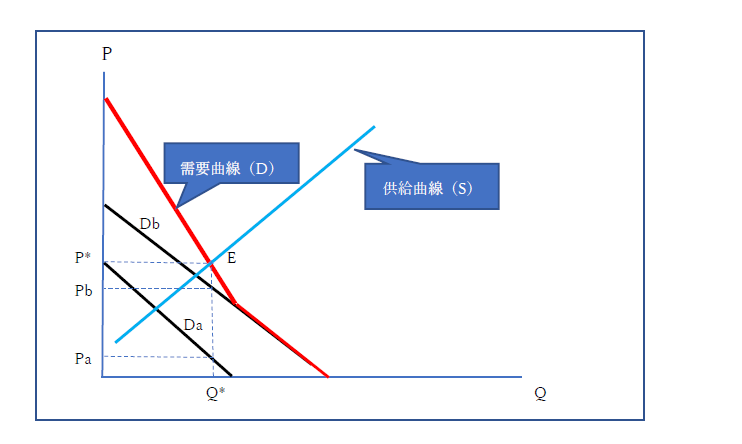
　図表のDaは、Aさんの公共財の需要関数を示します。Bさんの需要関数は、Dbです。

　図表上では、AさんよりBさんのほうが、より高い需要となっています。これに対して、2人の全体需要は、垂直に足し合わせたものなので、赤い線の需要関数（D）となります。このときに、公共財の最適供給の条件は、

　P*　＝　Pa　＋　Pb

　となります。

　ただし、PaもPbも、実際に購入した価格ではなく、あくまでもそれぞれが公共財に対して評価した便益の大きさを示したものです。ですから、厳密にいえば、限界評価の便益（MB）というべきですが、ここでは、一応、価格という表現を使っています。

　つぎに、供給曲線は、水色の線（供給曲線S）です。これは、政府や自治体が任意に供給するものです。ただし、これも先の限界概念を使えば、限界費用（MC）といえますが、ここでは、供給曲線という言葉を使っています。

　ここで、需要曲線と供給曲線より、均衡価格（P*）と均衡量（Q*）がE点で決定すると考えます。

　しかし、公共財の最適な供給は、大きな問題を抱えています。それを次回議論します。