第55回　生産関数

　ミクロ経済学は、消費者と生産者という２つの経済主体の行動を記述する学問です。

　すでに、企業の費用論は議論しましたが、ここからは「生産関数（production function）」論を何回かに分けてお話しします。

　この社会経済に、財やサービスを供給する経済主体は、企業です。現実の経済では、様々な種類の企業があるでしょうが、ミクロ経済学ではその種類は原則問いません。

　図表１がもっとも簡素な1経済主体の生産体制（構造）を示しています。

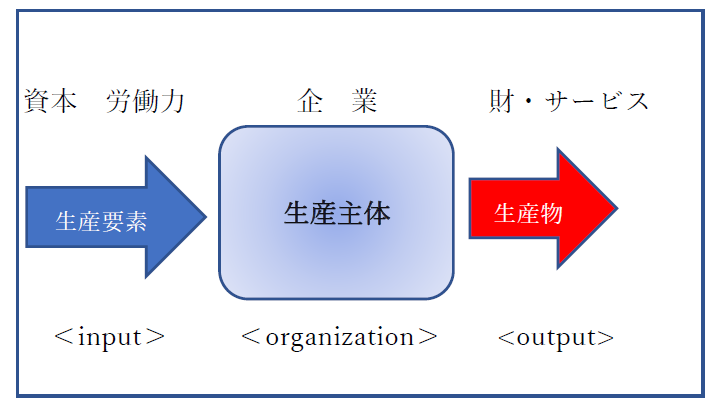
　財やサービスを生み出すためには、「生産要素(factor of production)」の投入が必要です。その生産要素のなかには、「固定インプット（fixed input）」と「可変インプット（variable input）」があります。固定インプットは、建物や機械などであり、費用論では、固定費用として考えていたものです。これに対して、可変インプットは、可変費用であり、原材料や光熱費などです。

　これを他の概念で示すと、「資本（capital）」と「労働力（labor）」といえます。

　式で示すと、

　Q　＝　ｆ（ K  ,  L ）     ・・・・①   　　 Q：生産量　K：資本　L：労働力

　です。

　資本と労働力を組み合わせて、生産物を生み出すということを示しています。

　図表１では、何らかの組み合わせの仕組みや構造が、生産様式であり、生産方法です。関数でいえば、「ｆ」がそれを示しています。より具体的にいえば、資源を組み合わせるノウハウや知識や技術などです。この関数がどのようなものかは、今後議論していきます。

　そこで生み出されたものが、「生産物（products）」です。図表でいえば、アウトプットです。

　つぎに、①式で、資本は固定して考えてみます。

　すると、

　と式を変形できます。これは、生産量が、労働力（Ｌ）のみによって、変化することを意味します。なお、労働力を固定して、資本を変数としても同様な変形となります。

　この労働力と生産量を図示したものが、図表２です。

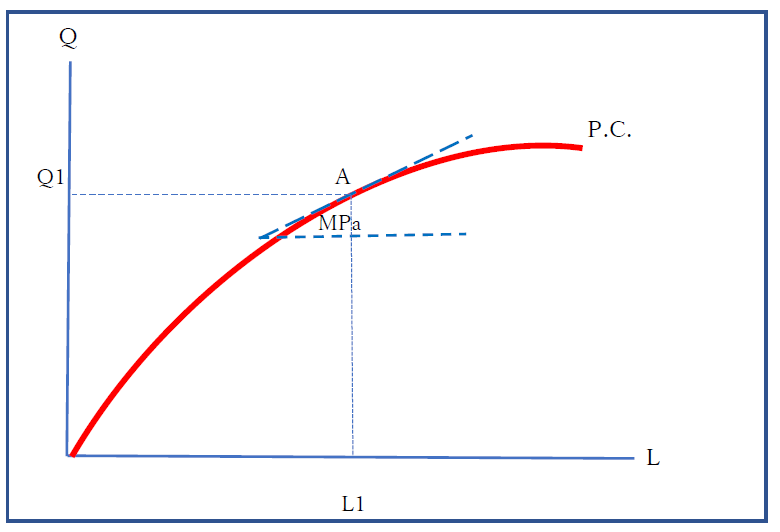
　図表2は、横軸に、労働力（Ｌ）をとり、縦軸に、生産量（Ｑ）をとっています。

　「生産物曲線（product Curve：P.C.）」は、図の赤い線です。

　この生産物曲線には、２つの特徴があります。

　その第一は、労働力が増加すると、必ず、生産量は増加するということです。曲線が上昇し続けることを示しています。

　第二は、労働力が増加するにしたがって、生産量の増加する割合が低下するということです。「生産要素である労働力を一単位投入したときに増加する生産量」を、「限界生産物（marginal product）」といいます。労働力の増加にしたがって、徐々に小さくなるので、「限界生産力逓減の法則（law of diminishing marginal productivity）」といいます。なお、図表２では、Ａ点での限界生産力（ＭＰa）が、青い破線の角として表されています。A点は、労働力Ｌ１と生産量Ｑ１を組み合わせたときの点で、限界生産力は、その点での「接線の傾き」ともいえます。

　以上の想定は、古典的な産業の労働力と生産量の関係を示しているといえますが、必ずしも、生産物曲線が図表２のようになるとはいえません。労働力が増加することによって、当初は生産性が高まり、その後は、低下するような場合は、Ｓ字曲線（ロジスティック曲線）のような形状が適切な場合もあります。

　たとえば、古典的な産業の例としては、農業があります。一定の農地に、農業従事者が増える場合、ひとりあたりの増加分は普通は低下するように思われます。それに対して、工業や複雑な産業では、Ｓ字曲線の方がふさわしいといえるかもしれません。

　ここでは、生産関数の最初の議論でしたので、古典的な事例を考えました。