第65回　最適消費点

　ここでは、2財の消費における「最適消費点(optimum consumption point)」を考えます。

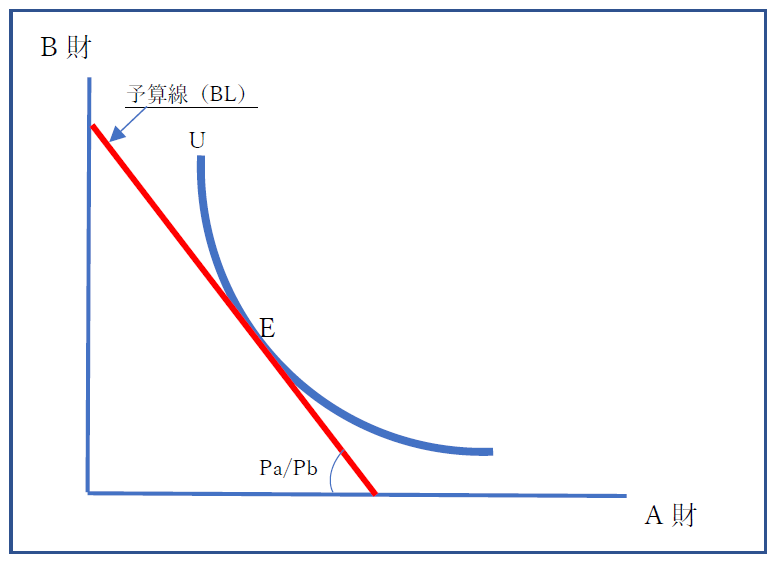
　前回お話をした無差別曲線が、図表のU曲線です。今一度述べますと、U曲線上の効用は同じなので、差別化されない曲線という意味で、無差別曲線と呼んでいます。

　横軸がA財の消費量で、縦軸がB財の消費量です。

　ここで、ミクロ経済学は、消費者であれ、生産者であれ、限られた資源（予算や費用）を使って、最適な量を導き出します。

　ここでは、消費者における問題なので、個々人の所得（家計）を考えます。

それを定式化すると、①式となります。

　I　＝　Pa・A　＋　Pb・B　　　　・・・・・・①

　（I:所得、Pa : A財の価格、A：A財の消費量、Pb：B財の価格、B：B財の消費量）

　この①式は、ある個人の予算線（BL: budget line）です。一定のI（所得）の中で、最大の消費を考えようとしています。予算線より下は購入可能ですが、予算を使い切っていない状態です。また、予算線以上は、購入不可能です。

　よって、予算すべてを使った最大の消費量は、E点となります。

この①式を変形すると、②式が得られます。

　B　=　－（Pa/Pb）A 　＋　I/Pb  ・・・・・②

　②式のAの係数は、②式の傾きを示しています。

　E点での接線の傾きは、前回みた「限界代替率（MRS）」でした。

　ここで、最適消費点の条件は、

　MRS　＝　Pa/Pb   ・・・・・・③

　となります。

　すなわち、無差別曲線と予算線が接するE点は、限界代替率と予算線の傾きが同じになることを意味しています。