第71回　ゼロサムゲーム

　今回は、「ゼロサムゲーム(zero-sum game)」または「ゼロ和ゲーム」と呼ばれるものを考えます。

　ここでも、以下のような利得表を使って論じていきます。　

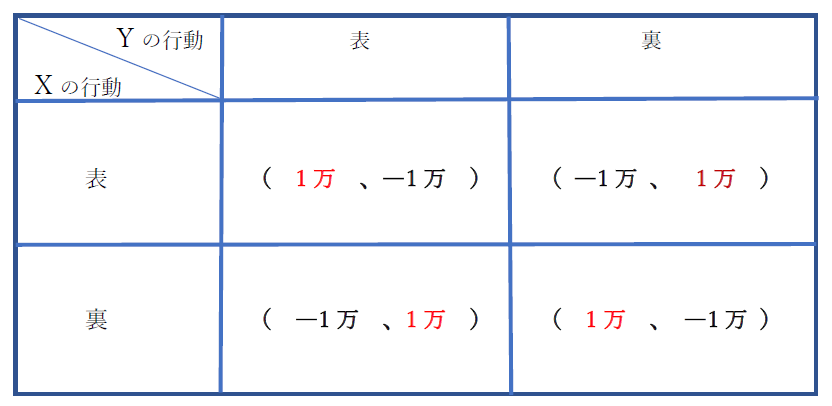
　ここで、ゼロサムゲームの戦略の前提としての構成要素を述べてみます。

　プレイヤーは、ゲームをする2名とします。それぞれが、コインを相手に見せないようして、表か裏にします。2枚ともが表または裏の場合は、Xが1万円を獲得し、2枚の表裏が合わない時は、Yが1万円をもらえるゲームとします。このようなゲームは、「マッチングペニー・ゲーム（matching penny game）」と呼ばれています。

　また、図表のような利得表があるとします。

　ここで、ナッシュ均衡であるかどうかを、前回同様の手順で判断すると、今回は、ナッシュ均衡は、存在しないことが分かります。また、XとYの利得を合わせると、「ゼロサム」（総和がゼロ）となっています。すなわち、２者の利得の合計は、ゼロなのです。

　このゲームの理論では、「ナッシュ均衡が必ずしもあるとは限らない」ことを示しています。

このゲームの場合、もともと、表裏の出方の確率は、2分の1ずつなので、結果、1万円得ることも、失うことも50％なのです。

なので、このようなゲームは、理論上、参加することが無意味なようにも思われます。期待効用計算でも、

EU(期待効用) ＝ 0.5×1万円　＋　0.5×（－1万円）　

　　　　　　 ＝ 0円

　となります。

　しかし、遊びとしての「小さい賭け」（まさにゲーム）は、いたるところでみられる行動（現象）です。遊びの要素として、ある学者は、「運不運」をあげています。運があるか無いかを試すこと自体に効用があるとすれば、結果は、金銭的にはゼロサムであり、期待効用がゼロでも、遊びの楽しみに何らかの効用があると考えれば、そのゲームに参加する誘因はあるといえるかもしれません。

　それを単純化して示すと、

遊びとしてのゼロサムゲーム ＝ （期待効用ゼロ）＋（あそびの効用α）＝　α

ともいえ、

　αが＋であれば、その分、ゲームに参加することは無意味ではないといえます。

　そもそもあらゆる遊びは、金銭にならないことが普通ですし、その遊びに何らかの効用があるからするということでしょう。