マクロ経済学第80回　成長会計

　今回から、経済成長論を書いていきます。

　この経済成長論も、理論形成の時系列にそってテキストでは書かれることが多いのですが、今回は、もっともよく使われる理論をまずみてみます。

　日本経済は、この30年間、経済成長率が低いことが課題となっていますが、これ以上成長しなくてもよいという見解もあります。しかし、国家の中で付加価値が増加しなければ、一人当たりの豊かさは実現しません。これに関して、富の分配比率を変えればいいという意見もあります。経済学では、所得の再配分論といいます。それはまた別の話です。

　最近、よく耳にする言葉に、SDGｓというのがあります。これは、「Sustainable Development Goals」の略で、日本語では、持続的発展目標と訳されています。この概念すら、持続的であるような社会調和のとれた発展なのです。やはり、発展（成長）なくては、これ自体の実現も不可能といえるでしょう。

　そこで、マクロ経済学では、経済成長論がまた注目を浴びています。

　そのなかで、新古典派のソロー(Robert M. Solow)の「成長会計(growth accounting)」を考えます。

　一国の経済成長が、どの要因から構成されているのかを簡潔に表現できる公式です。

　まず、一国に投入される生産要素を「資本(Capital)」と「労働(Labor)」と考えます。つぎに、それでは把握できないものを、「全生産性要素(TFP; Total Factor of Productivity)」とします。ここでは、Aと表現されています。

　様々な生産関数の中で、「コッブ＝ダグラス型生産関数(Cobb-Douglas function)」を用いて、その中に時間（ｔ）が入った形をとります。それが、第一式です。

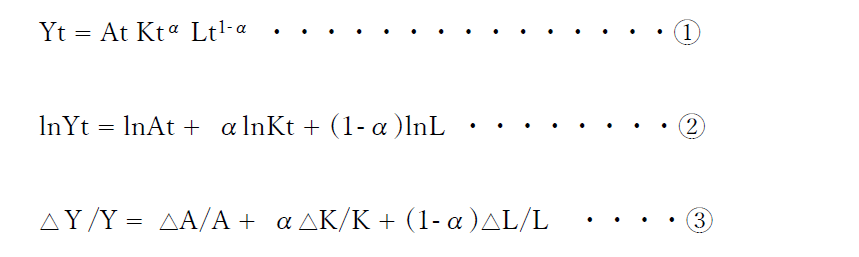
　第一式の両辺を対数にとったものが第二式です。さらに、それを微分したものが、第三式となります。

　第一式のαは、「資本分配率（capital share）」で、資本所得の割合を示し、（1-α）は、「労働分配率（labor share）」で、労働所得の割合を示しており、この合計は、1となるので、「規模に関して収穫一定（constant returns to scale）」を意味します。なお、（１-α）をβとして表すと、α + β = 1 、で表現されることもあります。

　第三式の左辺である（△Ｙ/Y）は、国民所得（GDP）の成長率（経済成長率）を表し、右辺の（△A/A）は、TFPの成長率、（α△K/K）は、資本分配率×資本の増加率、（(1-α)△L/L）は、労働分配率×労働の増加率を表しています。よって、経済成長率は、TFP成長率（技術進歩率）と資本成長率と労働成長率の合計で把握できることになります。

　ただし、（△A/A）は、測定が困難なので、経済成長率から、資本の寄与分と労働の寄与分を引いた残りとして計算されます。これを「ソロー残差（Solow residual）」といいます。

　このような表現でTFPを考えていいのかを巡って、経済成長論はいろいろな発展を遂げることになります。