第39回　限界費用と利潤最大化条件

　「限界費用（MC：Marginal Cost）」とは、「追加的一単位を生産するのに要した費用」のことです。他の言葉でいいかえると、「費用曲線上のある点の接線の傾き」のことです。　

　なので、TC線上のいたるところの点の接線の傾きとして表されます。

　下図表では、緑の線で表されています。

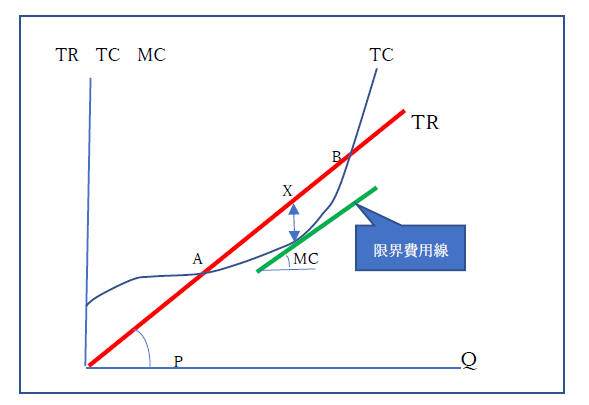
　図表をみると、A点までは、総収入曲線（TR）のほうが、総費用曲線（TC）よりも下にきているので、赤字の状態といえます。その後、A点からB点までは、収入のほうが費用よりも上回っているので、黒字の状態といえます。さらに、生産量が増え、B点を超えると、また赤字の状態となります。これからいえることは、企業には、小さすぎず大きすぎない生産が望まれているということです。

　では、利潤が最大になる条件を考えてみましょう。

　図表では、X点が、もっとも黒字幅が大きくなっているので、このXの生産量で利潤が最大化するといえます。

　ここで、利潤式からこのことを考えてみます。

　利潤　＝　収入　－　費用

　です。記号で表すと、

　π　＝　P×Q　－　C(Q)

　となります。

　ここで、Qについて、微分し、最大化条件を求めると、

　P　＝　MC

　となります。

　ここで、限界費用が出てきました。この式の意味しているところは、価格と限界費用が同じ時に利潤が最大化するということです。Pは、図表の収入曲線の傾きであり、MCは、接線の傾きです。それが同じ時に、黒字幅が最大となり、すなわち、利潤が最大となるのです。