第60回　様々な生産関数

　生産関数にもいろいろな型があります。

　数式を変形すれば、無限に異なる関数ができるでしょうが、ここでは、標準なテキストによく出てくる３つの生産関数の型を取り上げます。

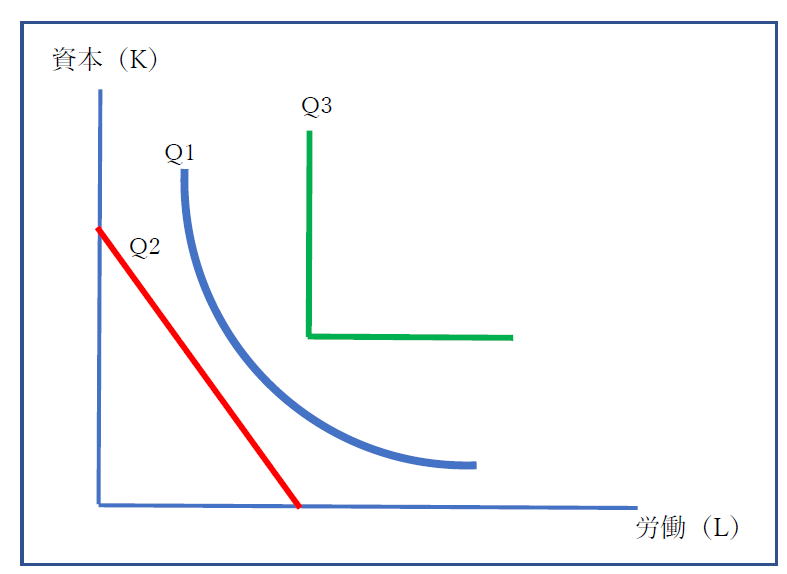
　第一は、これまでたびたび出てきた右下がりで原点に凸な関数です。

　これは、「コブ＝ダグラス型生産関数（Cobb-Douglas production function）」で、もっとも使われている関数です。

　図表1でいえば、Q1曲線の関数です。

　この関数は、図表２の数式①として、定式化されています。

　左辺Qは、生産量で、右辺のAは、ある係数です。これば大きければ大きいほど、Q1曲線は、右上方に移行します。アルファー（α）とベータ（β）は、それぞれの生産要素の係数です。ここでは、合計は、１となっています。つぎに、労働に関する限界生産力（MPL）は、①式を、労働量（L）について偏微分します。すると、②式が得られます。同じように、資本に関する限界生産力（MPK）は、③式のようになります。その比をとると、④式となります。

　第二は、「線形型生産関数（Linear produciton function）」です。図表1でいえば、Q２曲線（直線）です。

　これは、⑤式のように定式化できます。

　これの労働に関する限界生産力（MPL）は、⑥式であり、資本に関する限界生産力（MPK）は、⑦式であり、その比は、⑧式となります。

　第三は、「レオンチェフ型生産関数（Leontief production function）」です。　

　これは、図表1では、Q3曲線のように表現されます。L字型が特徴的です。

　定式化すると、⑨式となります。

　労働と資本の組み合わせのうちに、同じ生産量の場合、もっとも少ない生産要素を投入すると考えられるものです。この場合は、資本と労働の関係は、代替関係ではなく、補完関係であると考えています。

　これらをまとめますと、コブ＝ダグラス型生産関数は、資本と労働との関係が代替関係にあるととらえ、線形生産関数は、完全代替とみます。これに対して、レオンチェフ型生産関数では、資本が増加すると、労働も増加するという補完関係として生産要素を理解しているのです。