マクロ経済学第1回　消費関数について

　ミクロ経済学では、消費者の行動を理論的に把握しようとしてきましたが、消費と所得の関係について、あまり深くは論じていません。

　そこで、消費と所得の関係がどうなっているのかを考えるのが、消費関数論であり、様々な消費関数を巡って「消費関数論争」があります。

　ここでは、もっとも基本となる「消費関数(consumption function )」を考えることとしましょう。

　消費関数を定義づけると、「所得（Ｙ）の水準がきまると、それに対応する消費（Ｃ）の水準が一義的にきまるときの関係（Ｃ＝f(Ｙ）)」のことです（『経済学小辞典』岩波書店引用）。これを図示すると、以下の図表のようになります。

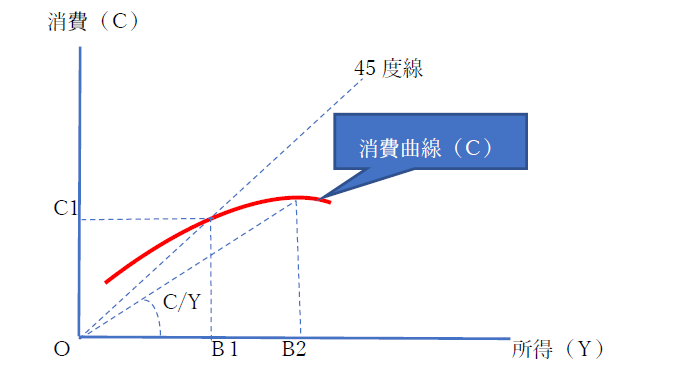
　図表１は、横軸に、所得（Ｙ）をとり、縦軸に、消費（Ｃ）をとっています。この図表のなかの45度線は、所得と消費が同じことを示しています。所得がＢ１よりも小さいときには、所得よりも消費が上回っており、貯蓄を取り崩しているか、借金をして生活していることを示しています。これに対して、Ｂ１よりも大きな所得の場合は、貯蓄が増えている状態となっています。ここで、消費曲線８（Ｃ曲線）が、赤い曲線のような形状だとすれば、以下のことが言えます。

　第１は、「平均消費性向（average propensity to consume）」は、所得の増加とともに、一方的に低下することを意味します。すなわち、所得の中に占める消費の割合が小さくなるのです。図表でいえば、Ｂ２における（Ｃ／Ｙ）のことを指します。

　第二は、 「限界消費性向（marginal propensity to consume）」、すなわち、所得の一単位の増加に対する消費の増加が逓減（△Ｃ/△Ｙ）していることを示しています。他の言葉で言い換えると、消費曲線に対する接線の傾きが逓減することを言うのです。

　これがもっとも基本となる消費と所得の関係を示しているものですが、戦後の実証的分析では、所得が増加しても、平均消費性向は低下しないことが明らかとなりました。ということは、図表のような消費関数は、現実の所得と消費の関係をうまく表現したものではないということになります。

　そこで、最初にあげた、消費関数論争が起きたのです。

　次回、標準的なマクロ経済学の消費関数として取り上げられているケインズの消費関数を検討していくことにします。